CV_札记

关于CS231n课的一些笔记

$L_i=-log(\frac{e^{f_y{_i}}}{\sum_je^{f_j}})$

$L=\frac{1}{N} \displaystyle \sum_i L_i + \frac{1}{2} \lambda \displaystyle\sum_k \displaystyle\sum_l W^{2}_{k,l}$

$\frac{\partial L_i}{\partial f_k} = p_k - \mathbb{ONE}(y_i=k)$

关于Hidden层的直觉性思考

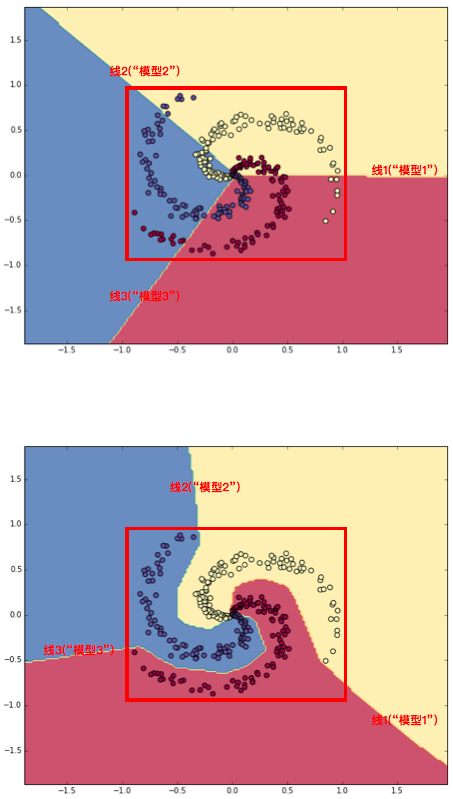
直觉性的理解: 对于输入空间中$x1$和$x2$不同取值, 隐藏层将它们原先的一次组合(即: 没有隐藏层的线性(vanilla)模型)进行”二次加工”, 比如: 输入数据点在第一层模型分类的基础上, 再次进行调整, 使得图1中的三条直线段在不同的取值区间(小范围内)内呈现不同的位移/扭曲(直线变曲线), 完成此例中的螺旋分类.

激活函数的加入, 使得原先的”线段式”曲线变得更平滑(消除了不同线段连接间的折角特征), 原先的”线段式”曲线变成真正的曲线(平滑的), 这像是一个消除图像马赛克的过程/模拟.

todo: 贴网络传导图

隐藏层对原线性模型的干预

好记性不如烂笔头(要理论, 也要工程):

1.jupyter notebook平常使用三步走: ;

matplotlib.plot三步走: ;

文字的先天不足: 文字就是文字, 在解释/描述程序世界时总是外界事物, 能用例子看懂了, 你还想要文字来描述吗: 编程语言的API再详细, 那也不是程序设计时的内在逻辑, 如https://matplotlib.org/api/_as_gen/matplotlib.pyplot.scatter.html?highlight=scatter#matplotlib.pyplot.scatter这个API的描述;

Matplotlib的API简记

首先, Matplotlib是因其作者想要在Python中使用像Matlab一样的画图(便利)方式而写出来的一个Python的画图库(主要是数据图的绘制而不是图像的显示/绘制, 图像的显示/绘制应该用OpenCV, 即cv2模块(但安装的时候是’pip install opencv-python’(或者python-opencv, 哪个对用哪个))), 此库的前三个字母就是Matlab的前三个字母, 接着是两个单词: plot(绘制)和lib(库). Matplotlib的pyplot模块最为常用: 体现为代码语句import matplotlib.pyplot as plt的使用频率.

在做cs231n中模型的总结时, 调用到其一些函数, 做个总结, 加深印象(第一个api我会写得详细一些, 其它的话都是一样的套路就不那么详细, 除非有新的要点出现):

plt.contourf()[REF]: 调用格式(Call signatures): contour([X, Y,] Z, [levels], **kwargs):

X和Y参数是数组(np.array())形式的变量(如: np.arange(9)), 代表的是平面坐标系中的两个维度上的坐标X和Y$^{[注1]}$, 调用时可以省略不给(它们在中括号([])中), 不给的话, 在函数内有默认的值(整数索引, “integer indices”)会被填充进去: X=range(M), Y=range(N), 即X从0到M-1, 以及Y从0到N.

X和Y是Z中元素值的坐标, 它们的维度要么是2D的, 或者要么是1D的(详见下图关于X,Y的说明).

Z参数是必须给的, 它的shape是(N,M), 对应len(Y)/Z的行数和len(X)/Z的列数, 即把X和Y相应位置的索引对应到相应的Z值(等高图中的高度).

注1: 经常弄错的是, 我把(x1,y1)当做参数X, 把(x2,y2)当做参数Y传给numpy函数, 但numpy中把所有X维度和Y维度上的一系列坐标分开处理, 只不过用相同的索引i将两个数组中的坐标对应起来(如X[1]对应Y[1]): 就是这样的, 轮子就是这样的.

说了这么多, 上图吧(一图胜千字):

01_CONTOURF参数API.png

图1: 参数说明

02_等高图.png
图2: 等高图例

contourf()函数在matplotlib库中的原代码为[REF]:

> @docstring.copy(Axes.contourf)
> def contourf(*args, data=None, **kwargs):
>     __ret = gca().contourf(
>         *args, **({"data": data} if data is not None else {}),
>         **kwargs)
>     if __ret._A is not None: sci(__ret)  # noqa
>     return __ret
>

在这个函数内部, 它调用的是gca().contourf(), 而gca()又return gcf().gca(**kwargs), 而gcf()$^{[注]}$的定义返回的是figManager.canvas.figure或者figure(), 至此, 终于好像看到了绘图的一线曙光了.

而figure()返回的是figManager.canvas.figure, 这就明白了: 如果在gcf()调用中, 有figManager.canvas.figure对象的存在, 则直接返回它, 如果没有此对象, 则调用figure(), 生成一个figManager.canvas.figure对象后返回它.

注: gcf()的意涵是: Get Current Figure, gca()的意涵是: Get the Current :class:~matplotlib.axes.Axes (instance on the
current figure matching the given keyword args, or create one)

函数返回的是: c(contour), 一个QuadContourSet对象, 详见[REF].

最后, contourf()的**kwargs参数在此函数页面的Other Parameters中被说明, 包含: corner_mask, colors, alpha, cmap, norm, vmin/vmax, origin, extent, locator, extend, xunits/yunits, antialiased, Nchunk, linewidths, linestyles, hatches.

作为contourf()API的总结结尾, 引用一个它的使用用例[REF]:

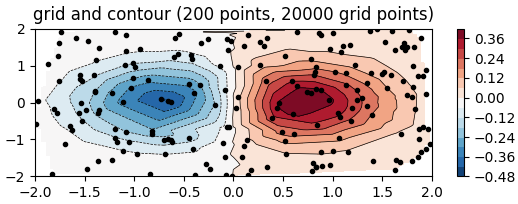
图3: Irregularly_Contour

Concise Pyplot Toturial - 简要Pyplot说明[REF]

An introduction to the pyplot interface.

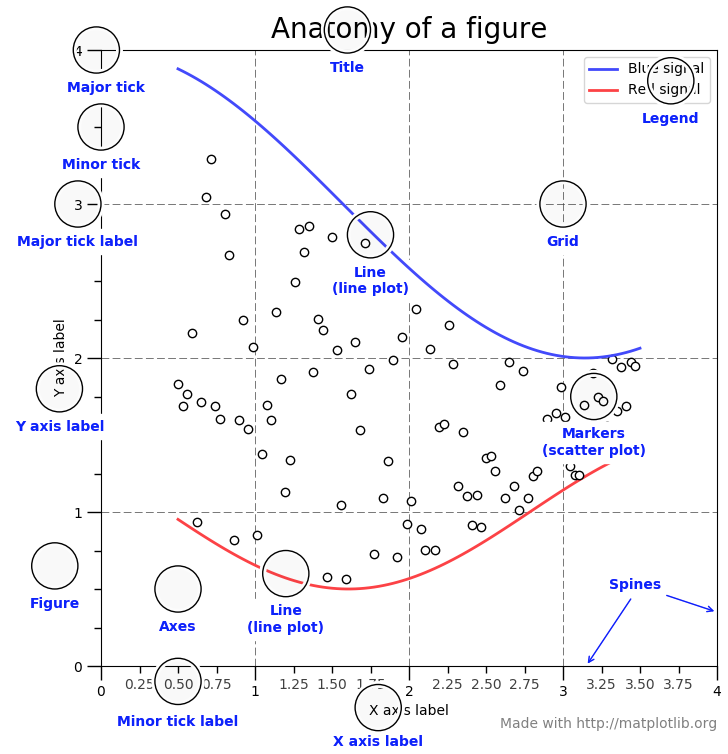
图: Part Of A Figure

首先, 我们常见的是: import matplotlib.pyplot as plt, 通过上述语句, 我们

MMM

快点来报道:

程序: 高级编程, CPU, 汇编.