斜率与梯度 关键词: 偏导数, 斜率, 多维空间的斜率, 梯度. 例子讲解: 我们有函数$Z=f(X,Y)$(如下图1), 通过此函数我们讲解斜率(偏导数)与梯度的具体异同. 此处, 个人觉得斜率的称谓适合在我们平常用的平面坐标系中(二维)中使用, 而在三维及以上的空间中, 就是偏导数了, 故也可以将偏导数理解成多维空间中的斜率.

图1.
关于这两者的应用, 个人有个疑惑: 为什么梯度下降中, 我们要减去梯度项, 但如果此时斜率本身就是小于0的, 减去这一项岂不是让值增加了?! 如: $w := w - \alpha \nabla_wf(w)$, 此处, 我们将上述表述中的每一项理清:
- 我们有下图2中红点处的一斜率/梯度, 其值<0, 我们要梯度下降, 就是让函数值$Z$下降(亦: 损失函数函数值$Loss$);
- 我们减去此梯度值($w - \alpha \nabla_wf(w)$), 被减数是$w$(并不是函数值$Z$), 则实际$w$值增加了, 对于整个函数来说, 其值是减少的;
- 此处, 我混淆了两个细节:
- 被减数是$w$而不是函数值$Z$, 通过$w$的增加, 从而使$Z$值减少;
- 在形如$WX+b$的常用模型中, $W$是我们要学习的模型参数, 又是我们偏导的对象(易理解成变量)(你也可以对$X$求偏导, 但那没意义), 而$X$是输入(易理解成常量), 我们怎么可以去改变变量的值呢, 它是不固定的呀(要不断改变接收新值), 上面这个想法正是我混淆的根源. 上面, 我是惯性了我的思维了, 就像$y=f(x)$那样, 觉得$W$就像$x$那样就是不断变化的;
- 总结: 其实我们的$W$和$X$都是变量, 对于$W$, 我们变化它是为了寻找到一个适合输入数据$X$的一组值, 而对于$X$, 则本身就是不同的有变化的数据.
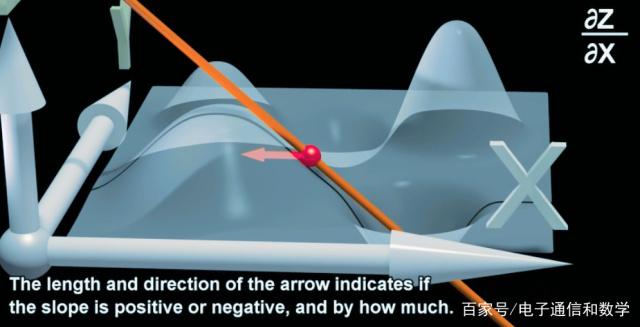
图2. (梯度不完全等同于倾斜度: $tan(\alpha)=b:a$)
以上图例具体在结合反向传播的梯度时, 应在细节上做一下区分, 要不然会混淆却说不出具体原因, 在对模型WX+b进行求偏导时, 我们的模型参数W既是偏导的对象(情形1), 也是模型在预测时相对于输入X的有确定值的系数(情形2):
在情形1中, 我们对每一个$W$分量($w1$, $w2$, …)进行偏导运算, 此时, 对$W$的理解应是”它是变量”, 我们得到了整个函数(损失函数)在每个$W$分量上的斜率, 而梯度则往往是简略的说法, 在斜率的基础上乘以一个单位值1就成了梯度, 此时它们的值相等, 但概念不等. 我们把这个梯度加回到该分量$w1$中回去, 则对应上图中(红点处斜率<0)的$X$轴的$x$值变小了, 则整个函数(损失函数)值变大了, 而我们减去这个梯度, 就是减小了损失函数值.
更多细节是: 梯度并不能完全重合与曲面(以上图为例), 在加了一次梯度改变$w1$(对应图中$x$维度)的值后, 模型(指参数$W$)也改变了, 故下次我们需重新计算斜率(即偏导, 即epoch), 获取新的梯度再次更新模型(参数$W$), 而学习率, 动量, 自适应动量, 局部最优等概念, 都是上图中的细节.
在情形2中, 模型将不被用于训练和求偏导而是用来求值, 此时, 可将模型的参数$W$理解成输入X的系数, 将$X$理解成变量(因为输入$X$是变化着的不同样本), 由于前期进行了训练, 我们的模型参数$W$有了确定了的合理的值(假设是合理的话, 当然, 模型没训练前也有值), 此时, 再将$W$作为求偏导的分量对象(如$w1$)就不太好理解了.
以上, 总结了梯度和斜率中我混淆的地方, 它们也是ML数学和常用数学使我混淆的地方: 如$X$在ML中是输入(像常量)而常用数学中$x$是自变量.
(P.S. CV心得: 别跟我说什么CV, 我只认数学结构和技巧, 只不过这些因素被你们人类拿去当做CVision了, 这锅我(数学)不背: C中根本没有V, 是人类的Romantic裹挟了我数学)
https://baijiahao.baidu.com/s?id=1627719346341492607&wfr=spider&for=pc