RCNN: Rich Feature Hierarchies For Accurate Object Detection And Semantic Segmentation
0.背景
<<精准目标检测和语义分割中的丰富特征层级>> 这篇论文的主要意义可以说是利用深度学习(CNN)进行目标检测的开山之作. 现在的目标检测算法主要有两类: 1.基于候选区域(RegionCNN), 2.基于端到端(YOLO, SSD).
下面, 我将认为重要的要点总结出来, 以巩固熟悉算法, 但总结的要点并不代表论文的全部.
1.鸟瞰模型整体
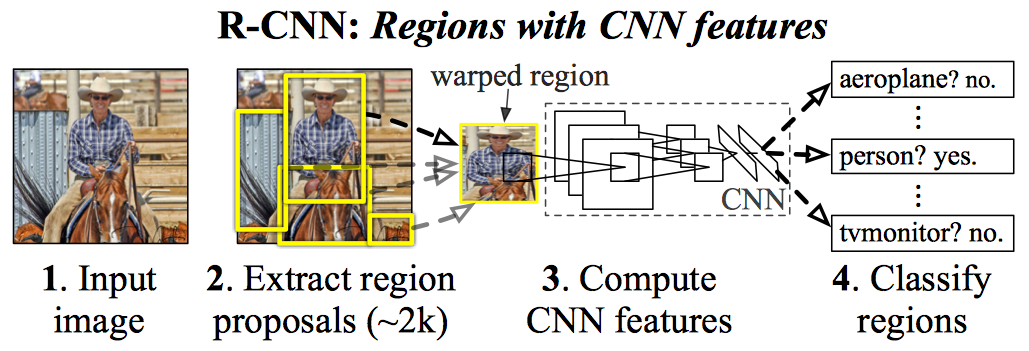
图1: 模型鸟瞰
首先, 贴出上图, 给出模型中区域特征提取的流程, 后续理解与解释则围绕图片展开. 我们有如下步骤:
Input image: 这是RCNN模型的输入数据, 我们要识别此输入图片中的物体与其在图片中的位置(坐标);
候选区域的抽选: 通过Selective Search算法, 在图片中抽取出约2000个候选区域(图片的子图, 大小不一);
计算出特征: 此特征是CNN网络(论文中用了AlexNet)的输出特征(pool5), 上一步骤的大小不一的候选区域, 在这一步的卷积前, 需要变形(warp)到AlexNet的(227*227)的输入尺寸;
SVM分类: 在上一步得到AlexNet输出的抽象特征后, 用SVM将这些特征进行类别分类, 如果RCNN模型要分类20种的对象, 则需要21(20种物体+1个背景)个SVM进行分类, 至于为什么不用AlexNet后面的3个全连接层, 论文也有讨论.
对图片中任意位置对象的分类完成后, 我们还需要定位对象在图中的位置, 论文中也有讲述Bounding box的回归训练, 这在论文的附录C中详细叙述.
2.论文第二节: Object detection with R-CNN
论文将它的对象检测系统(object detection system)分为3个部分:
- 类别无关(category-independent)的候选区域生成;
- 为每个候选区域生成固定长度(fixed-length)的特征向量;
- 一组用于分类的(线性)SVM.
模型设计1: 候选区域(Region Proposals)
论文中提到了一系列用于生成(不关类别)候选区域的方法(罗列如下), 其中, 论文使用的是selective search方法:
- objectness
- selective search(论文选用)
- category-independent object proposals
- constrained parametric min-cuts(CPMC)
- multi-scale combinatorial grouping
- Ciresan et al.
而, 至于候选区域生成方法具体是如何工作的, 论文中并没有说明.
模型设计2: 特征抽取(Feature Extraction)
模型中SVM使用的特征是一个4096维的feature vector, 它是每个候选区域通过AlexNet的前向传播(forward propagating)得到的结果(你看, 此篇论文将目标检测和深度网络结合了). 由于候选区域是不管你AlexNet要227*227尺寸的输入的, 它只产生它认为有意义的区域作为候选(Proposal), 所以, 我们需要对这些候选区域做一个图片的变形(warp, 即拉伸), 原文和我理解的拉伸方式如下(理解了很久, 烧了不少脑细胞):
Regardless of the size or aspect ratio of the candidate region, we warp all pixels in a tight bounding box around it to the required size. Prior to warping, we dilate the tight bounding box so that at the warped size there are exactly p pixels of warped image context around the original box (we use p = 16).
估计即便将以上论文片段翻译成中文, 如果仅凭中文字面意思去理解, 也无解, 所以还是画图吧(如果论文中有配图就好了):

图2: 边框示意
在上图中, 我们有里面的小框, 即我们的tight bounding box(也即候选区域). 由于候选区域是原图的一部分, 如果我们要在使around the original box的pixel为16的话, 则向外扩张(dilate)数标1中的原框(Original T. B. Box)16个像素值, 得到数标2中的Dilated T. B. Box, 而这个有原图的context填充(padding)了的Boundxing Box, 就是我们要resize(即warp)到227*227的”候选区域”(而不是里面的那个了). 如果候选区域图中上下左右方向不够Padding的话, 则用灰度像素替代吧, 具体细节可参考论文中的Figure 7. (再次的, 觉得这是论文的小瑕疵: 没有图呀)
Appendix C- Bounding-box Regression
下面, 讲讲论文中边界框的回归(即定位). 我估计论文之所以没有在正文中讲边界框的回归定位而是在附录中讲, 是因为之前的候选区域抓取的时候已经有了该候选区域的坐标值了, 而这一步, 只是提升用的:
原文: We use a simple bounding-box regression stage to improve localization performance.
回归与数据: 论文在使用了SVM进行区域内内容的class-specific detection后, 开始使用class-specific bounding-box regressor来预测边界框(bounding box)了, 并提及, 此边界框回归和DPM(Deformable Part Models)模型中的边界框回归思想类似. 然而, 它们的不同之处是两者使用的数据来源, 论文中边界框回归使用的数据是CNN输出的特征(向量), 而DPM使用的数据是geometric features computed on the inferred DPM part locations.
公式符号设置:
$\{(P^i,G^i)\}_{i=1,…,N}$: 表示N组训练数据对, 其中, $P^i=(P^i_x,P^i_y,P^i_w,P^i_h)$代表第i个候选区域在整张原图的中心点坐标(x,y)以及它的宽和高(w,h). 同理, G符号代表的则是真实框(Ground Truth)对应的四个像素位置坐标值: $G=(G_x,G_y,G_w,G_h)$(此处省略上标 i).
Transformation:
- $d_x(P)$, $d_y(P)$: 边界框中心的位移(高宽比不变, scale-invariant);
- $d_w(P)$, $d_h(P)$: 边界框高宽变化的转换(log-space translation);
- $\hat G$: 转换后的predicted ground-truth box.
$\hat G$具体公式:
$\hat G_x=P_wd_x(P)+P_x$
$\hat G_y=P_hd_y(P)+P_y$
$\hat G_w=P_wexp(d_w(P))$
$\hat G_h=P_hexp(d_h(P))$
通过以上计算, 则有了我们在(x,y,w,h)四个维度上对真实值的预测了, 下面, 我们要计算这个预测G值与真实G值. 我们有一个参数向量$W_*$, 它是用于学习的的可调参数, 有:
$d_(P)=W^T_\phi_5(P)$, 其中$\phi_5(P)$是pool5层产生的特征向量
则关于最优$W_*$的公式为如下公式, 其中加号后面的一项是L2正则项(least squares objective), 故此回归也是岭回归(ridge regression):
$W_ = argmin_{\hat W_} \displaystyle \sum^{N}_{i}(t^i_-\hat W^T_\phi_5(P^i))^{2}+\lambda||\hat W_*||^2$
另外, 还有对关于训练数据(P, G)的回归目标$t_*$的定义:
- $t_x=(G_x-P_x)/P_w$
- $t_y=(G_y-P_y)/P_h$
- $t_w=log(G_w/P_w)$
- $t_h=log(G_h/P_h)$
直觉地理解上面的目标项, 就是让训练参数$W$尽量去拟合pool5层特征值和G数据与P数据在(x,y)上的位移值和在(w,h)上的缩放值, 这样, CNN的特征值与位移/缩放就关联上了, 目标检测中的定位问题也就完成了.
在此附录C末尾, 作者提到两点细微的问题:
- 正则化在此处对模型是重要的: 论文设置了$\lambda=1000$, 在评估数据中(validation set);
- 选择(P, G)数据对时需选择两者相距不远的(not far from), 否则这个转换就没什么意义了(transform P to G does not make sense), 个人觉得, 这是因为如果一个P相距所有的G都太远, 则说明这个候选区域P本身就是没有选对的(selective search这一步只是把所有候选区域选出来, 当然会选出不含目标的区域), 故不应将P和G关联. 以上只是我的一个猜想推理.
以上, 论文的部分讲解与理解.
行内与独行
- 行内公式:将公式插入到本行内,符号:,如:$xyz$
- 独行公式:将公式插入到新的一行内,并且居中,符号:xyz$$
上标、下标与组合
- 上标符号,符号:
^,如:$x^4$ - 下标符号,符号:
_,如:$x_1$ - 组合符号,符号:
{},如:${16}_{8}O{2+}_{2}$
汉字、字体与格式
- 汉字形式,符号:
\mbox{},如:$V_{\mbox{初始}}$ - 字体控制,符号:
\displaystyle,如:$\displaystyle \frac{x+y}{y+z}$ - 下划线符号,符号:
\underline,如:$\underline{x+y}$ - 标签,符号
\tag{数字},如:$\tag{11}$ - 上大括号,符号:
\overbrace{算式},如:$\overbrace{a+b+c+d}^{2.0}$ - 下大括号,符号:
\underbrace{算式},如:$a+\underbrace{b+c}_{1.0}+d$ - 上位符号,符号:
\stacrel{上位符号}{基位符号},如:$\vec{x}\stackrel{\mathrm{def}}{=}{x_1,\dots,x_n}$
占位符
- 两个quad空格,符号:
\qquad,如:$x \qquad y$ - quad空格,符号:
\quad,如:$x \quad y$ - 大空格,符号
\,如:$x \ y$ - 中空格,符号
\:,如:$x : y$ - 小空格,符号
\,,如:$x , y$ - 没有空格,符号``,如:$xy$
- 紧贴,符号
\!,如:$x ! y$
定界符与组合
- 括号,符号:
()\big(\big) \Big(\Big) \bigg(\bigg) \Bigg(\Bigg),如:$()\big(\big) \Big(\Big) \bigg(\bigg) \Bigg(\Bigg)$ - 中括号,符号:
[],如:$[x+y]$ - 大括号,符号:
\{ \},如:${x+y}$ - 自适应括号,符号:
\left \right,如:$\left(x\right)$,$\left(x{yz}\right)$ - 组合公式,符号:
{上位公式 \choose 下位公式},如:${n+1 \choose k}={n \choose k}+{n \choose k-1}$ - 组合公式,符号:
{上位公式 \atop 下位公式},如:$\sum_{k_0,k_1,\ldots>0 \atop k_0+k_1+\cdots=n}A_{k_0}A_{k_1}\cdots$
四则运算
- 加法运算,符号:
+,如:$x+y=z$ - 减法运算,符号:
-,如:$x-y=z$ - 加减运算,符号:
\pm,如:$x \pm y=z$ - 减甲运算,符号:
\mp,如:$x \mp y=z$ - 乘法运算,符号:
\times,如:$x \times y=z$ - 点乘运算,符号:
\cdot,如:$x \cdot y=z$ - 星乘运算,符号:
\ast,如:$x \ast y=z$ - 除法运算,符号:
\div,如:$x \div y=z$ - 斜法运算,符号:
/,如:$x/y=z$ - 分式表示,符号:
\frac{分子}{分母},如:$\frac{x+y}{y+z}$ - 分式表示,符号:
{分子} \voer {分母},如:${x+y} \over {y+z}$ - 绝对值表示,符号:
||,如:$|x+y|$
高级运算
- 平均数运算,符号:
\overline{算式},如:$\overline{xyz}$ - 开二次方运算,符号:
\sqrt,如:$\sqrt x$ - 开方运算,符号:
\sqrt[开方数]{被开方数},如:$\sqrt[3]{x+y}$ - 对数运算,符号:
\log,如:$\log(x)$ - 极限运算,符号:
\lim,如:$\lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}$ - 极限运算,符号:
\displaystyle \lim,如:$\displaystyle \lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}$ - 求和运算,符号:
\sum,如:$\sum^{x \to \infty}_{y \to 0}{\frac{x}{y}}$ - 求和运算,符号:
\displaystyle \sum,如:$\displaystyle \sum^{x \to \infty}_{y \to 0}{\frac{x}{y}}$ - 积分运算,符号:
\int,如:$\int^{\infty}_{0}{xdx}$ - 积分运算,符号:
\displaystyle \int,如:$\displaystyle \int^{\infty}_{0}{xdx}$ - 微分运算,符号:
\partial,如:$\frac{\partial x}{\partial y}$ - 矩阵表示,符号:
\begin{matrix} \end{matrix},如:$\left[ \begin{matrix} 1 &2 &\cdots &4\5 &6 &\cdots &8\\vdots &\vdots &\ddots &\vdots\13 &14 &\cdots &16\end{matrix} \right]$
逻辑运算
- 等于运算,符号:
=,如:$x+y=z$ - 大于运算,符号:
>,如:$x+y>z$ - 小于运算,符号:
<,如:$x+y<z$ - 大于等于运算,符号:
\geq,如:$x+y \geq z$ - 小于等于运算,符号:
\leq,如:$x+y \leq z$ - 不等于运算,符号:
\neq,如:$x+y \neq z$ - 不大于等于运算,符号:
\ngeq,如:$x+y \ngeq z$ - 不大于等于运算,符号:
\not\geq,如:$x+y \not\geq z$ - 不小于等于运算,符号:
\nleq,如:$x+y \nleq z$ - 不小于等于运算,符号:
\not\leq,如:$x+y \not\leq z$ - 约等于运算,符号:
\approx,如:$x+y \approx z$ - 恒定等于运算,符号:
\equiv,如:$x+y \equiv z$
集合运算
- 属于运算,符号:
\in,如:$x \in y$ - 不属于运算,符号:
\notin,如:$x \notin y$ - 不属于运算,符号:
\not\in,如:$x \not\in y$ - 子集运算,符号:
\subset,如:$x \subset y$ - 子集运算,符号:
\supset,如:$x \supset y$ - 真子集运算,符号:
\subseteq,如:$x \subseteq y$ - 非真子集运算,符号:
\subsetneq,如:$x \subsetneq y$ - 真子集运算,符号:
\supseteq,如:$x \supseteq y$ - 非真子集运算,符号:
\supsetneq,如:$x \supsetneq y$ - 非子集运算,符号:
\not\subset,如:$x \not\subset y$ - 非子集运算,符号:
\not\supset,如:$x \not\supset y$ - 并集运算,符号:
\cup,如:$x \cup y$ - 交集运算,符号:
\cap,如:$x \cap y$ - 差集运算,符号:
\setminus,如:$x \setminus y$ - 同或运算,符号:
\bigodot,如:$x \bigodot y$ - 同与运算,符号:
\bigotimes,如:$x \bigotimes y$ - 实数集合,符号:
\mathbb{R},如:$\mathbb{R}$ - 自然数集合,符号:
\mathbb{Z},如:$\mathbb{Z}$ - 空集,符号:
\emptyset,如:$\emptyset$
数学符号
- 无穷,符号:
\infty,如:$\infty$ - 虚数,符号:
\imath,如:$\imath$ - 虚数,符号:
\jmath,如:$\jmath$ - 数学符号,符号
\hat{a},如:$\hat{a}$ - 数学符号,符号
\check{a},如:$\check{a}$ - 数学符号,符号
\breve{a},如:$\breve{a}$ - 数学符号,符号
\tilde{a},如:$\tilde{a}$ - 数学符号,符号
\bar{a},如:$\bar{a}$ - 矢量符号,符号
\vec{a},如:$\vec{a}$ - 数学符号,符号
\acute{a},如:$\acute{a}$ - 数学符号,符号
\grave{a},如:$\grave{a}$ - 数学符号,符号
\mathring{a},如:$\mathring{a}$ - 一阶导数符号,符号
\dot{a},如:$\dot{a}$ - 二阶导数符号,符号
\ddot{a},如:$\ddot{a}$ - 上箭头,符号:
\uparrow,如:$\uparrow$ - 上箭头,符号:
\Uparrow,如:$\Uparrow$ - 下箭头,符号:
\downarrow,如:$\downarrow$ - 下箭头,符号:
\Downarrow,如:$\Downarrow$ - 左箭头,符号:
\leftarrow,如:$\leftarrow$ - 左箭头,符号:
\Leftarrow,如:$\Leftarrow$ - 右箭头,符号:
\rightarrow,如:$\rightarrow$ - 右箭头,符号:
\Rightarrow,如:$\Rightarrow$ - 底端对齐的省略号,符号:
\ldots,如:$1,2,\ldots,n$ - 中线对齐的省略号,符号:
\cdots,如:$x_1^2 + x_2^2 + \cdots + x_n^2$ - 竖直对齐的省略号,符号:
\vdots,如:$\vdots$ - 斜对齐的省略号,符号:
\ddots,如:$\ddots$
https://www.cnblogs.com/peaceWang/p/Markdown-tian-jia-Latex-shu-xue-gong-shi.html